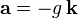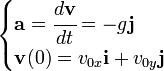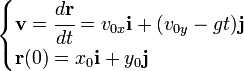simulador de tiro parabolico
jose luis suarez arteaga, 24 Enero 2013, Creado con GeoGebra |
El salto de longitud y el tiro parabolico
Vistas de página en total
miércoles, 17 de abril de 2013
EL SIMULADOR DE TIRO PARABOLICO PARA PODER USARSE
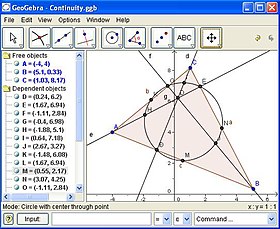
QUE ES GEOGEBRA....
GeoGebra
 GeoGebra es un software matemático interactivo libre para la educación en colegios y universidades. Su creador Markus Hohenwarter, comenzó el proyecto en el año 2001 en la Universidad de Salzburgo y lo continúa en la Universidad de Atlantic, Florida.
GeoGebra es un software matemático interactivo libre para la educación en colegios y universidades. Su creador Markus Hohenwarter, comenzó el proyecto en el año 2001 en la Universidad de Salzburgo y lo continúa en la Universidad de Atlantic, Florida.
Es básicamente un procesador geométrico y un procesador algebraico, es decir, un compendio de matemática con software interactivo que reúne geometría, álgebra y cálculo, por lo que puede ser usado también en física, proyecciones comerciales, estimaciones de decisión estratégica y otras disciplinas.
Su categoría más cercana es software de geometría dinámica.
Con GeoGebra pueden realizarse construcciones a partir de puntos, rectas, semirrectas, segmentos, vectores, cónicas, etc., mediante el empleo directo de herramientas operadas con el ratón o la anotación de comandos en la Barra de Entrada, con el teclado o seleccionándolos del listado disponible -. Todo lo trazado es modificable en forma dinámica: es decir que si algún objeto B depende de otro A, al modificar A, B pasa a ajustarse y actualizarse para mantener las relaciones correspondientes con A.
GeoGebra permite el trazado dinámico de construcciones geométricas de todo tipo así como la representación gráfica, el tratamiento algebraico y el cálculo de funciones reales de variable real, sus derivadas, integrales, etc
Funcionamiento
Flash de pantalla en Microsoft Windows XP
0. Para documentar detalladamente la operatoria, conviene consultar el Manual Oficial en Español / Castellanohttp://www.geogebra.org/help/docues.pdf accesible desde la página de Centro Babbage http://www.centrobabbage.com/soft.htm
1. Dibujo de Polígonos: Para dibujar un polígono
Para dibujar un polígono cualquiera, basta con seleccionar la herramienta correspondiente e ir estableciendo la posición en la Vista Gráfica, de cada uno de sus puntos vértices, volviendo a señalar el primero después del último. Si se prefiriera un polígono regular, hay que recurrir a la herramienta que aparece bajo la anterior, a la que se tiene acceso con un clic sobre el triangulito al pie a la derecha de la primera. Esta maniobra despliega, en cada caso, todas las herramientas disponibles bajo la que encabeza las de cada tipo. Con la herramienta para el trazado de polígonos regulares activada, basta con establecer en la Vista Gráfica la posición de los puntos vértices de uno de los lados y luego indicar el número de puntos vértices en la caja de diálogo que se despliega.
2. Transferencia de Medidas: Trazamos un segmento AB de medida a, esta medida se puede transferirse a partir de cualquier punto de la Vista Gráfica, libre o de otra figura (recta, segmento, semirrecta, vector). Lo usual con útiles geométricos convencionales es emplear el compás: haciendo centro en el punto desde el que se quiere establecer el segmento para trazar la circunferencia de radio a y decidir cuál de sus puntos será el otro extremo del segmento que se procura -uno u otro de los puntos de intersección de la recta sobre la que se quiere dibujar, por ejemplo - para trazar el segmento desde el centro a tal punto. Esta misma maniobra puede llevarse adelante con GeoGebra, ocultando, al finalizar, los elementos auxiliares como la circunferencia o dándole un estilo adecuado, punteado, y/o de color más pálido-. De hecho, GeoGebra cuenta con herramientas ajustadas a la trasferencia de la medida de un segmento en estos términos: Compás - si se cuenta con el segmento cuya longitud se desea transferir y se decide luego el centro - y Circunferencia dados su Centro y Radio - si se desea dejar establecido el punto centro y se conoce el valor de la medida o se puede indicar el nombre del segmento cuya longitud se desea transferir-.
Una alternativa sería trazar tal segmento a, entre el punto de inicio elegido en b (la recta, semirrecta o segmento b) y el punto final obtenido al trasladar el inicial según un vector de magnitud a y recta de acción b Traslada[P_{inicial}, a VectorUnitario[b]]
[editar]Exportación
Los proyectos pueden ser exportados en diversos formatos. Los applets dinámicos se pueden publicar directamente en GeoGebraTube2 o exportar a HTML (e incluirlo en ambientes educativos virtuales3 como Moodle). También es posible exportar a SVG, que puede ser editado por otros programas (como Inkscape), o EMF que se puede importar en numerosasaplicaciones ofimáticas. Otras formatos posibles son PNG, PDF, EPS, PGF/TikZ y Asymptote.
GeoGebra también puede generar código utilizable en archivos LaTex a fin de crear las mismas imágenes que muestra GeoGebra, a través del paquete PSTricks, PGF/TikZ o Asymptote.
[editar]Licencia
La mayor parte del programa de GeoGebra es distribuido con licencia GPL o CC-BY-SA,4 por lo que es software libre.
[editar]Premios
- Tech Awards Distinción en Tecnología 2009 (Silicon Valley, EE. UU.)5
- EASA 2002: European Academic Software Award (Ronneby, Suecia)6
- Learnie Award 2003: Austrian Educational Software Award (Viena, Austria)
- Digita 2004: German Educational Software Award (Colonia, Alemania)7
- Comenius 2004: German Educational Media Award (Berlín, Alemania)8
- Learnie Award 2005: Austrian Educational Software Award for Andreas Lindner (Viena, Austria)9
- Les Trophées du Libre 2005: International Free Software Award, category Education (Soisson, Francia
TEORIA EN CINEMATICA APLICADA AL PARABOLICO
Movimiento parabólico (completo)
El movimiento parabólico completo se puede considerar como la composición de un avance horizontal rectilíneo uniforme y un lanzamiento vertical hacia arriba, que es un movimiento rectilíneo uniformemente acelerado hacia abajo (MRUA) por la acción de la gravedad.
En condiciones ideales de resistencia al avance nulo y campo gravitatorio uniforme, lo anterior implica que:
- Un cuerpo que se deja caer libremente y otro que es lanzado horizontalmente desde la misma altura tardan lo mismo en llegar al suelo.
- La independencia de la masa en la caída libre y el lanzamiento vertical es igual de válida en los movimientos parabólicos.
- Un cuerpo lanzado verticalmente hacia arriba y otro parabólicamente completo que alcance la misma altura tarda lo mismo en caer.
[editar]Ecuaciones del movimiento parabólico
Hay dos ecuaciones que rigen el movimiento parabólico:
donde:
 es el módulo de la velocidad inicial.
es el módulo de la velocidad inicial. es el ángulo de la velocidad inicial sobre la horizontal.
es el ángulo de la velocidad inicial sobre la horizontal. es la aceleración de la gravedad.
es la aceleración de la gravedad.
La velocidad inicial se compone de dos partes:
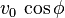 que se denomina componente horizontal de la velocidad inicial.
que se denomina componente horizontal de la velocidad inicial.
- En lo sucesivo

- En lo sucesivo
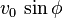 que se denomina componente vertical de la velocidad inicial.
que se denomina componente vertical de la velocidad inicial.
- En lo sucesivo
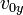
- En lo sucesivo
Se puede expresar la velocidad inicial de este modo:
 : [ecu. 1]
: [ecu. 1]
Será la que se utilice, excepto en los casos en los que deba tenerse en cuenta el ángulo de la velocidad inicial.
[editar]Ecuación de la aceleración
La única aceleración que interviene en este movimiento es la constante de la gravedad, que corresponde a la ecuación:
que es vertical y hacia abajo.
[editar]Ecuación de la velocidad
La velocidad de un cuerpo que sigue una trayectoria parabólica se puede obtener integrando la siguiente ecuación:
La integración es muy sencilla por tratarse de una ecuación diferencial de primer orden y el resultado final es:
| [mostrar]
Derivación de la ecuación de la velocidad
|
|---|
Esta ecuación determina la velocidad del móvil en función del tiempo, la componente horizontal no varía, mientras que la componente vertical sí depende del tiempo y de la aceleración de la gravedad.
[editar]Ecuación de la posición
Partiendo de la ecuación que establece la velocidad del móvil con la relación al tiempo y de la definición de velocidad, la posición puede ser encontrada integrando de la siguiente ecuación diferencial:
La integración es muy sencilla por tratarse de una ecuación diferencial de primer orden y el resultado final es:
| [mostrar]
Derivación de las ecuación de la posición
|
|---|
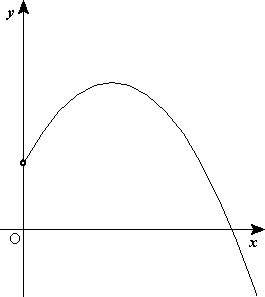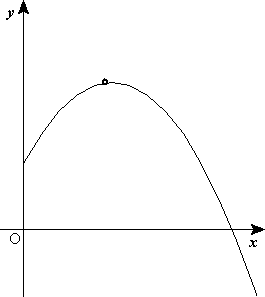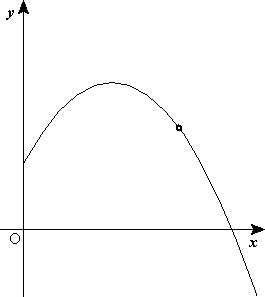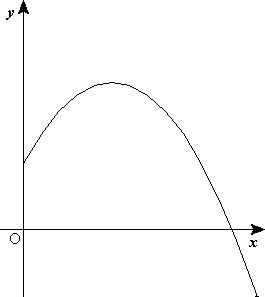
La trayectoria del movimiento parabólico está formada por la combinación de dos movimientos, uno horizontal de velocidad constante, y otro vertical uniformemente acelerado; la conjugación de los dos da como resultado una parábola.
Suscribirse a:
Comentarios (Atom)